정렬 알고리즘 총정리

0. 들어가며

정렬 알고리즘은 시간 복잡도에 따라 성능이 좌우되며, 성능이 좋을 수록 구현 방법이 어려워진다

 

O(n²)의 시간 복잡도 (정렬할 자료의 수가 늘어나면 제곱에 비례해서 증가)

• 버블 정렬(Bubble Sort)
• 선택 정렬(Selection Sort)
• 삽입 정렬(Insertion Sort)

O(n log n)의 시간 복잡도

• 병합 정렬(Merge Sort)
• 퀵 정렬(Quick Sort)
• 셸 정렬

 

1. 버블 정렬

버블정렬은 인접한 두 수를 비교하며 정렬해나가는 방법으로 O(n²)의 느린 성능을 가지고 있다.

 

주요 처리 과정

• 앞에서부터 (2개씩 비교를 )시작하여 큰 수를 뒤로 보내, 뒤가 가장 큰 값을 가지도록 완성해나가는 방법이다.
  • 한바퀴 돌면, 가장 오른쪽 원소는 최대값으로 fix될테니, 고정시켜두고, 그 앞 인덱스(위 그림에선 7) 까지 다시 처음부터 반복
  • 뒤에서부터 반복하여 앞의 작은 값부터 정렬을 완성해나가는 방법도 있다!

 

수도코드

 

파이썬 예제코드

def bubble_sort(arr):
    n = len(arr)
    for i in range(n-1): 
        print("i: " ,  i)
        for j in range(n-i-1):
            if arr[j] > arr[j+1]:
                arr[j],arr[j+1] = arr[j+1],arr[j]
                print("sorting: ",arr)
        print(arr)

array = [9,8,7,6,5,4,3,2,1]
print("before: ",array)
bubble_sort(array)
print("after: ",array)

 

c++ 예제코드

 

#include <iostream>
#include <vector>
#include <string>
#include <cstring>
using namespace std;

void BubbleSort(vector<int>& arr) {
    int n = arr.size();
    for (int i = 0; i < n - 1; i++) {
        cout << "i: " << i << endl;
        for (int j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                swap(arr[j], arr[j + 1]);
                cout << "sorting: ";
                for (int elem : arr) {
                    cout << elem << " ";
                }
                cout << endl;
            }
        }
        cout << "Array state: ";
        for (int elem : arr) {
            cout << elem << " ";
        }
        cout << endl;
    }
}

int main() {
    vector<int> array = {9, 8, 7, 6, 5, 4, 3, 2, 1};
    cout << "before: ";
    for (int elem : array) {
        cout << elem << " ";
    }
    cout << endl;
    
    BubbleSort(array);
    
    cout << "after: ";
    for (int elem : array) {
        cout << elem << " ";
    }
    cout << endl;

    return 0;
}

 

 

2. 선택 정렬

 

주요 처리 과정

• 1번째부터 끝까지 훑어서 가장 작은 게 1번째 -> 2번째부터 끝까지 훑어서 가장 작은 게 2번째 -> 정렬이 끝날 때까지 반복
• 이미 정렬되어 있는 자료구조에 삽입/제거 할 때나 배열이 작은 경우에는 매우 효율적이다.
• 앞에서부터 정렬해나가는 특성을 가지고 있으므로 > 버블 정렬과 마찬가지로 최악의 성능을 가진 알고리즘이다.

 

시간복잡도

• Avg: O(n^2) → 이중 for
• Worst: O(n^2)
• Best: O(n^2)

 

 

 

 

파이썬 예제 코드

def selection_sort(arr):
    n = len(arr)
    for i in range(n):
        min_idx = i
        for j in range(i+1,n):
            if arr[j] < arr[min_idx]:
                min_idx = j
        arr[i],arr[min_idx] = arr[min_idx],arr[i]
        print(arr[:i+1])
    

array = [9,8,7,6,5,4,3,2,1]
print("before: ",array)
selection_sort(array)
print("after: ",array)

 

결과

before:  [9, 8, 7, 6, 5, 4, 3, 2, 1]
[1]
[1, 2]
[1, 2, 3]
[1, 2, 3, 4]
[1, 2, 3, 4, 5]
[1, 2, 3, 4, 5, 6]
[1, 2, 3, 4, 5, 6, 7]
[1, 2, 3, 4, 5, 6, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 8, 9]
after:  [1, 2, 3, 4, 5, 6, 7, 8, 9]

 

3. 삽입 정렬

 

주요 처리 과정

• k번째 원소를 1부터 k-1까지와 비교해(k기준 왼쪽 값들이) 적절한 위치에 끼워넣고, 그 뒤의 자료를 한 칸씩 뒤로 밀어내는 방식이다.
• 버블 정렬과 선택 정렬과 마찬가지로 최악의 성능인 정렬 알고리즘이다.

→ 삽입정렬은 2번째 인덱스부터 시작!

→ 현재 인덱스는 별도의 변수 x에 저장해주고, 비교 인덱스(=j)를 현재인덱스 i 에서 1칸 뒤에있는, i-1로 잡는다

 

시간 복잡도

• Avg: O(n^2)
• Worst: O(n^2)
• Best: O(n)

파이썬 예제 코드

array = [8,4,6,2,9,1,3,7,5]

def insertion_sort(arr):
    n = len(arr)
    for i in range(1,n):
        for j in range(i,0,-1):
            if arr[j-1] > arr[j]:
                arr[j-1],arr[j] = arr[j],arr[j-1]
        print(arr[:i+1])

print("before: ",array)
insertion_sort(array)
print("after:", array)

 

결과

before:  [8, 4, 6, 2, 9, 1, 3, 7, 5]
[4, 8]
[4, 6, 8]
[2, 4, 6, 8]
[2, 4, 6, 8, 9]
[1, 2, 4, 6, 8, 9]
[1, 2, 3, 4, 6, 8, 9]
[1, 2, 3, 4, 6, 7, 8, 9]
[1, 2, 3, 4, 5, 6, 7, 8, 9]
after: [1, 2, 3, 4, 5, 6, 7, 8, 9]

 

 

4. 병합 정렬

병합 정렬은 하나의 리스트를 두 개의 균등한 크기로 분할하고, 분할된 부분 리스트를 정렬한 다음, 두 리스트를 합하여 전체가 정렬된 리스트를 만드는 방법이다

 

• [1,4] [2,3] (1과 2 비교) -> 1 선택, 완성된 배열은 [1]
• [4] [2,3] (4와 2 비교) -> 2 선택, 완성된 배열은 [1,2]
• [4] [3] (4와 3 비교) -> 3 선택, 완성된 배열은 [1,2,3]
• [4] [] -> 남는 4 선택, 완성된 배열은 [1,2,3,4]

주요 처리 과정

 

병합 정렬의 주요 처리과정은 다음과 같다.

1. 분할(Divide): 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.(배열의 크기가 8→4→2→1로 줄어들었음.)
2. 정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면, 순환호출을 이용하여 다시 분할 정복 기법(1번)을 적용한다. 배열의 크기가 1이면 이미 정복된 것이다.
3. 병합(Combine,merge) : 정렬된 부분 배열들을 하나의 배열에 통합한다

 

파이썬 코드 구현

 

방식1)

def merge_sort(arr):
  if len(arr)<2:
    return arr
  
  mid = len(arr)//2
  left_arr = arr[:mid]
  right_arr = arr[mid:]
  
  left_arr = merge_sort(left_arr)
  right_arr = merge_sort(right_arr)
  
  return merge(left_arr,right_arr)

def merge(left_arr,right_arr):
  sorted_arr = []
  i,j = 0,0
  while i < len(left_arr) and j < len(right_arr):
    if left_arr[i] < right_arr[j]:
      sorted_arr.append(left_arr[i])
      i+=1
    elif left_arr[i] > right_arr[j]:
      sorted_arr.append(right_arr[j])
      j+=1
    
  # 왼,오 중 하나라도 끝나면 while문 종료되고, 남은 배열은 아직 sorted에 들어가지 않은 채 남아있게 됨
  
  while i<len(left_arr):
    sorted_arr.append(left_arr[i])
    i+=1
  while j < len(right_arr):
    sorted_arr.append(right_arr[j])
    j+=1
    
  return sorted_arr

arr = [21,10,22,30]
t = merge_sort(arr)   
print(t)

 

방식 2)

 

def merge_sort(S):
    if len(S) > 1:
        mid = len(S) // 2
        U = S[:mid]
        V = S[mid:]

        merge_sort(U)
        merge_sort(V)

        i = j = k = 0
        while i < len(U) and j < len(V):
            if U[i] < V[j]:
                S[k] = U[i]
                i += 1
            else:
                S[k] = V[j]
                j += 1
            k += 1

        while i < len(U):
            S[k] = U[i]
            i += 1
            k += 1

        while j < len(V):
            S[k] = V[j]
            j += 1
            k += 1

# Example usage:
S = [12, 11, 13, 5, 6, 7]
merge_sort(S)
print("Sorted array is:", S)

 

 

5. 퀵 정렬

 

퀵 정렬은

기준 데이터를 설정하고 그 기준보다 큰 데이터와 작은 데이터의 위치를 바꾸는 방법이다

• 일반적인 상황에서 가장 많이 사용되는 정렬 알고리즘 중 하나이다
• 병합 정렬과 더불어 대부분의 프로그래밍 언어의 정렬 라이브러리의 근간이 되는 알고리즘이다
• 가장 기본적인 퀵 정렬은 첫 번째 데이터를 기준 데이터(Pivot)로 설정한다

 

동작 예시

 

[Step 0] 현재 피벗의 값은 '5'이다. 왼쪽에서부터 '5'보다 큰 데이터를 선택하므로 '7'이 선택되고오른쪽에서부터 '5'보다 작은 데이터를 선택하므로 '4'가 선택된다. 이제 이 두 데이터의 위치를 서로 변경한다

 

 

 

[Step 1] 현재 피벗의 값은 '5'이다. 왼쪽에서부터 '5'보다 큰 데이터를 선택하므로 '9'가 선택되고오른쪽에서부터 '5'보다 작은 데이터를 선택하므로 '2'가 선택된다. 이제 이 두 데이터의 위치를 서로 변경한다

 

 

 

[Step 2] 현재 피벗의 값은 '5'이다. 왼쪽에서부터 '5'보다 큰 데이터를 선택하므로 '6'이 선택되고오른쪽에서부터 '5'보다 작은 데이터를 선택하므로 '1'이 선택된다. 단, 이처럼 위치가 엇갈리는 경우 '피벗'과'작은 데이터'의 위치를 서로 변경한다

 

 

 

[분할 완료] 이제 '5'의 왼쪽에 있는 데이터는 모두 5보다 작고, 오른쪽에 있는 데이터는 모두 '5'보다 크다는특징이 있다. 이렇게 피벗을 기준으로 데이터 묶음을 나누는 작업을 분할(Divide)이라고 한다

 

 

 

[왼쪽 데이터 묶음 정렬] 왼쪽에 있는 데이터에 대해서 마찬가지로 정렬을 수행한다

 

 

 

 

[오른쪽 데이터 묶음 정렬] 오른쪽에 있는 데이터에 대해서 마찬가지로 정렬을 수행한다

• 이러한 과정을 반복하면 전체 데이터에 대해서 정렬이 수행된다

 

 

파이썬 예제코드

def quickSort(arr,start,end):
  if start >=end: #원소가 1개인 경우, 종료
    return
  pivot = start
  left = start+1
  right = end
  
  while (left <= right):
    while(left <= end and arr[left] <= arr[pivot]): #pivot보다 큰 값 찾을 때까지 반복
      left +=1
    while (right > start and arr[right] >= arr[pivot]):
      right-=1
    if (left>right): #엇갈렸다면, 작은 데이터와 피봇을 교체
      arr[right],arr[pivot] = arr[pivot],arr[right]
    else:  # 엇갈리지 않았다면 작은 데이터와 큰 데이터를 교체
      arr[left],arr[right] = arr[right],arr[left]
  
  # 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬 수행
  quickSort(arr,start,right-1)
  quickSort(arr,right+1,end)
  
arr = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]
quickSort(arr,0,len(arr)-1)
print(arr)

 

 

 

6. 힙 정렬

힙 정렬은 힙 트리 구조를 이용하는 정렬 방법이다.

최소힙 → 내림차순 정렬에 사용

최대힙 → 오름차순 정렬에 사용

 

힙(heap) 이란?

부모 노드의 값이 자식 노드의 값보다 큰 완전이진트리를 의미한다! 힙 상태와 힙이 아닌 상태를 아래 그림으로 이해해보자

 

 

 

 

주요 처리 과정

• 부모 노드의 값이 자식 노드의 값보다 항상 크기 때문에 힙의 루트에는 제일 큰 수가 들어가게 된다.
• 이를 이용하여 힙의 루트 값을 꺼내어 배열의 오른쪽부터 채워넣으면서(오름차순 기준) 배열을 정렬할 수 있다.
• 힙으로 만들기 -> 배열의 맨 오른쪽부터 루트값 채워넣기 -> 다시 힙으로 만들기 -> 루트값 채워넣기  ...

-> 이렇게 배열의 정렬이 완료될 때까지 힙 만들기와 루트값 넣기를 반복하여 정렬을 한다.

 

 

시간 복잡도 : O(NlogN)

 

• 힙으로 만들 때 걸리는 시간 복잡도는 O(NlogN)
• 힙에서 루트값을 꺼내는데 걸리는 시간 복잡도는 O(1) 

=> 힙 정렬의 시간 복잡도는 O(NlogN)이 된다.

 

 

동작 예시

 

1) 힙이 아닌 트리를 힙 상태로 바꾸기

2)  힙(heap) -> 정렬하기

 

배열 arr의 요소가 5 9 3 1 8 6 4 7 2 일 때, 이 배열을 오름차순으로 정렬해보자!

배열 arr을 트리 형태로 나타내면 다음과 같다.

 

 

오른쪽 트리는 아직 힙 상태가 아니다. 부모 노드의 값이 자식 노드의 값보다 작은 경우가 존재하기 때문이다.

따라서 우선 오른쪽의 트리를 힙 상태로 바꿔줘야 한다.

 

힙이 아닌 트리를 힙 상태로 바꾸기

힙이 아닌 것을 힙으로 만들기 위해서 아래(Bottom)에서부터 위(Up)로 올라가며 힙 상태인지 아닌지 체크한다.

-> 만약에 힙 상태가 아니라면 왼쪽 자식 노드 값과 오른쪽 자식 노드 값을 비교하여 더 큰 값과 부모 노드 값을 교환한다.

 

트리의 아래부터 위로 올라가면서 힙 상태가 아닌 것을 찾아보자!

아래 그림에서 빨간색 박스(n//2 -1부터 시작) 안의 트리는 힙 상태가 아니다. 부모 노드의 값이 1로, 자식 노드 값인 2와 7보다 작기 때문이다.

 

 

 

그러면 자식 노드끼리 비교해보자.

왼쪽 노드의 값은 7, 오른쪽 노드의 값은 2 이므로 왼쪽 노드의 값이 더 크다.

그러므로 왼쪽 노드와 부모 노드를 서로 교환해준다.

 

1과 7을 교환함으로써 힙 상태가 되었다.

 

 

다음으로 아래의 빨간 박스 안의 트리를 보자.

역시 마찬가지로 부모 노드의 값이 3으로, 자식 노드값인 6과 4보다 작으므로 힙 상태가 아니다.

방금전과 마찬가지로 자식노드끼리 비교해서 더 큰 값과 부모노드를 교환하면 힙 상태로 바뀐다.

 

 

 

 

이제 올라가서 위쪽을 보면 빨간 박스 안의 부분트리가 힙 상태가 아니다.

자식 노드 값인 9와 6을 비교하면 9가 더 크므로 왼쪽 자식 노드와 부모 노드를 교환한다.

 

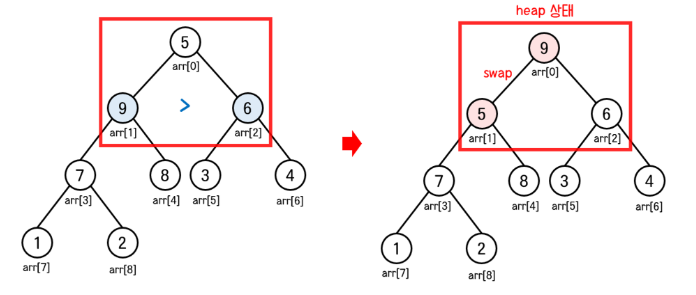
위의 9와 5가 교환됨에 따라 아래의 빨간 박스 부분이 힙 상태가 아니게 된다. 이 부분의 코드는 아래와 같다.

if largest != i:
	arr[i], arr[largest] = arr[largest], arr[i] # 변경된 노드에서 재귀적으로 heapify 호출 
    heapify(arr, n, largest)

 

 

동일한 방법으로 힙으로 만들어 주면 다음과 같다.

 

 

 

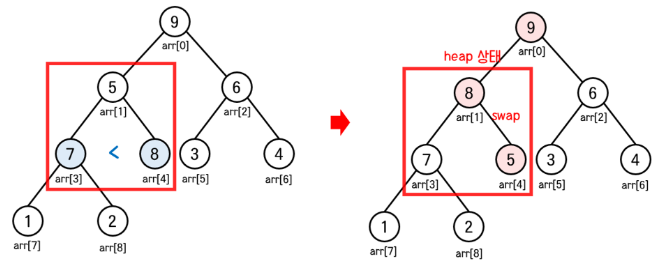
힙-> 정렬하기

이제 배열 전체를 힙 상태로 만들었다.

아래의 힙에서 루트에 있는 값인 9가 전체 중에서 가장 큰 값이 된다. 배열의 첫번째 요소에 가장 큰 값이 위치한다.

 

 

 

 

오름차순으로 정렬해야 하므로(최대힙은 오름차순 정렬인듯) 루트에 있는 가장 큰 값이 배열의 맨 오른쪽에 있어야 한다.

그러므로 arr[0] = 9를 arr[8] = 2와 서로 교환한다.

 

 

 

 

 

배열의 맨 오른쪽 9는 정렬이 완료되었다.(회색칸은 정렬이 완료되었음을 의미)

이제 9를 제외한 arr[0] ~ arr[7] 까지를 다시 힙 상태로 만들면(heapify 호출) 9 다음으로 큰 값인 8이 루트 노드에 위치하게 된다.

루트 노드에 있는 8을 arr[7] 로 옮기기 위해서 arr[0]과 arr[7]을 교환한다.

 

 

 

 

다시 힙으로 만들면(heapify호출) 루트 노드에 7이 들어간다.

arr[0]을 arr[6]의 값과 교환한다.

 

 

 

다시 힙으로 만들면 루트 노드에 6이 들어간다.

arr[0]을 arr[5]의 값과 교환한다.

 

 

 

다시 힙으로 만들면 루트 노드에 5가 들어간다.

arr[0]을 arr[4]의 값과 교환한다.

 

 

 

다시 힙으로 만들면 루트 노드에 4가 들어간다.

arr[0]을 arr[3]의 값과 교환한다.

 

 

 

 

다시 힙으로 만들면 루트 노드에 3이 들어간다.

arr[0]을 arr[2]의 값과 교환한다.

 

 

 

 

다시 힙으로 만들면 루트 노드에 2가 들어간다.

arr[0]을 arr[1]의 값과 교환한다.

 

 

 

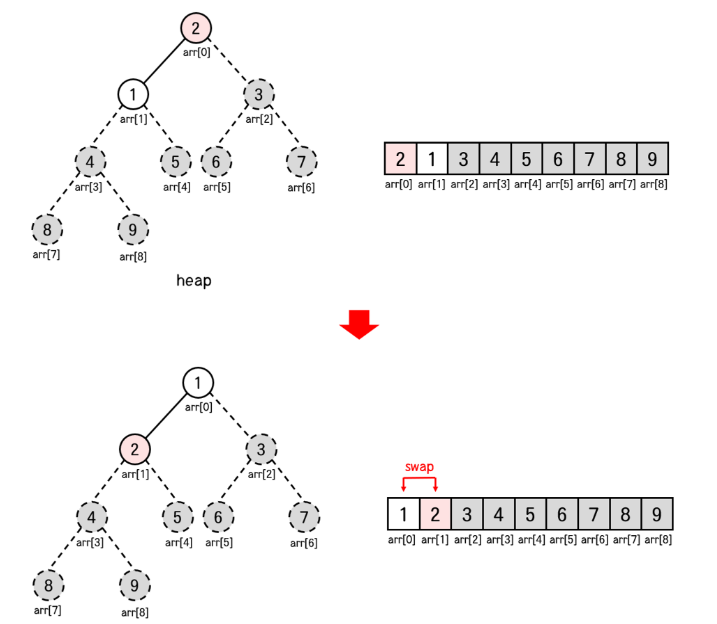
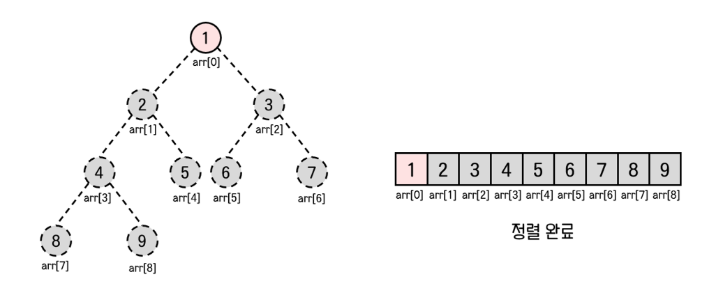
arr[1] 까지 정렬을 완료하고 나면 위 과정을 종료한다.

이런식으로 반복적으로 힙을 만들어서 배열을 오름차순으로 정렬할 수 있다.

 

 

 

 

 

파이썬 구현코드

 

최소힙 구현코드

def heapify(arr,parent_idx,n):
    smallest = parent_idx
    left_child = 2 * parent_idx + 1
    right_child = 2 * parent_idx + 2
    if (left_child < n and arr[left_child] < arr[smallest]):
        smallest = left_child
    if (right_child < n and arr[right_child] < arr[smallest]):
        smallest = right_child
    

    if smallest != parent_idx:#index상으로 뭔가 바뀐게 있다면
        arr[parent_idx],arr[smallest] = arr[smallest],arr[parent_idx] # 실제 값도 바꿔주고
        heapify(arr,smallest,n) #바뀐 것에 대해서도 최소힙 진행(가장 루트 말고)
        


def heap_sort(arr):
    n = len(arr)
    #최소 힙 정렬
    for i in range(n//2 - 1, -1,-1):
        heapify(arr,i,n)
    for i in range(n-1,0,-1):
        arr[i],arr[0] = arr[0],arr[i] #root와 가장 마지막 요소를 바꾸고 나서,
        heapify(arr,0,i) # 변경된 heap에서 다시 최소 heap 구성

    
        
# 테스트
arr = [12, 11, 13, 5, 6, 7]
print("정렬 전 배열:", arr)
heap_sort(arr)
print("정렬 후 배열:", arr)

 

최대힙 구현코드

def heapify(arr,parent_idx,n):
    largest = parent_idx
    left_child = 2 * parent_idx + 1
    right_child = 2 * parent_idx + 2
    if (left_child < n and arr[left_child] > arr[largest]):
        largest = left_child
    if (right_child < n and arr[right_child] > arr[largest]):
        largest = right_child
    

    if largest != parent_idx:#index상으로 뭔가 바뀐게 있다면
        arr[parent_idx],arr[largest] = arr[largest],arr[parent_idx] # 실제 값도 바꿔주고
        heapify(arr,largest,n) #바뀐 것에 대해서도 최소힙 진행(가장 루트 말고)
        


def heap_sort(arr):
    n = len(arr)
    #최소 힙 정렬
    for i in range(n//2 - 1, -1,-1):
        heapify(arr,i,n)
    for i in range(n-1,0,-1):
        arr[i],arr[0] = arr[0],arr[i] #root와 가장 마지막 요소를 바꾸고 나서,
        heapify(arr,0,i) # 변경된 heap에서 다시 최소 heap 구성

    
        
# 테스트
arr = [12, 11, 13, 5, 6, 7]
print("정렬 전 배열:", arr)
heap_sort(arr)
print("정렬 후 배열:", arr)

 

C++ 구현 코드

#include <iostream>
using namespace std;

void heapify(int a[], int h, int m) {
    int v = a[h];
    int j;
    for (j = 2*h; j <= m; j = j*2) {
        if (j < m && a[j] < a[j+1]) j++; //오른쪽노드 당첨 ( 2*h + 1)
        if (v >= a[j]) break; #지금 부모노드값보다 자식이 이미 작거나같으면, 넘어가~
        else { //현재 노드가 자식 노드보다 작다면
            a[j/2] = a[j]; // 현재노드와 자식 노드의 위치를 교환(현재 노드의 값을 자식 노드의 값으로 교체)
        } //j/2 는 현재노드의 인덱스
    }
    a[j/2] = v;
} 

void heapSort(int a[], int n) {
    for (int i = n / 2; i >= 1; i--) {
        heapify(a, i, n);
    }
    for (int i = n - 1; i >= 1; i--) {
        int temp = a[1];
        a[1] = a[i + 1];
        a[i + 1] = temp;
        heapify(a, 1, i);
    }
}

int main() {
    int a[] = {0, 4, 1, 3, 2, 16, 9, 10, 14, 8, 7};
    int n = sizeof(a) / sizeof(a[0]) - 1; // 배열의 크기 계산
    heapSort(a, n);
    cout << "정렬된 배열: ";
    for (int i = 1; i <= n; i++) {
        cout << a[i] << " ";
    }
    return 0;
}

 

 

 

7. 셸 정렬

삽입 정렬의 장점은 살리고 단점은 보안하여 좀 더 빠르게 정렬하는 알고리즘이다.

• 셸 정렬은 배열 전체를 한꺼번에 정렬하지 않고 일종의 전처리를 한다
  • 이것은 맨 마지막에 배열 전체를 정렬(삽입 정렬)해야 할 때 많은 항목들이 이미 자신의 자리 근처에 있도록 만드는 과정으로, 이를 통해 처리 시간을 줄이고자 한다

 

주요 처리 과정

1. 리스트를 일정한 기준에 따라 여러 개의 부분 리스트로 나눈다
2. 각 부분 리스트를 삽입 정렬을 이용해 정렬
3. 모든 부분 리스트가 정렬되면, 다시 전체 리스트를 더 적은 개수의 부분 리스트로 만든다
4. 앞 과정 되풀이

여기에서, 부분리스트란?

• 각 부분 리스트는 전체 리스트에서 거리가 k만큼 떨어진 요소들로 이루어진다
• 이 k를 간격(gap)이라 하고, 부분 리스트의 개수와 같다
• 셸 정렬은 큰 간격으로 시작해서 각 단계마다 간격 k를 줄이는데, 간격이 줄 수록 하나의 부분리스트에 속하는 요소의 갯수는 많아진다.

 

셸 정렬 동작 예시

1) 간격 k = 5

 

2) 간격 k = 3

 

 

3) 간격 k =1

2) 를 통해 정렬된 배열은 전체가 하나의 부분리스트 {1,3,2,4,8,5,6,9,7}인 상태로, 이미 많은 부분이 정렬되어있는 상태이다. 이제, 간격을 1로 삽입정렬을 진행한다.

대부분 1~2번의 비교만으로 삽입 위치를 찾는다. 셸 정렬은 이 효과를 노린다