[그래프 순회] DFS(깊이 우선 탐색, Depth-First Search)

DFS 알고리즘이란?

DFS(Depth-First Search)란 깊이 우선 탐색이라고도 불리며 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이다.

 

 

DFS 알고리즘 작동 과정

1. 정점 i를 방문한다.
2. 정점 i에 인접한 정점 중에서 아직 방문하지 않은 정점이 있으면, 이 정점들을 모두 스택에 저장한다.
3. 스택에서 정점을 삭제하여 새로운 i를 설정하고, 단계 (1)을 수행한다.
4. 스택이 공백이 되면 연산을 종료한다

 

배열 visited[n]을 이용하여, 정점의 방문 여부를 표시한다
- visited[i] = True : 방문하였음

- visited[i] = False: 방문하지 않음

 

 

BFS 알고리즘 작동 예시

 

0. visited배열 전부 False로 초기화

 

1. stack에 시작 원소 삽입

 

 

 

 

2. 스택에서 값 j 꺼낸 후, 방문 처리

 

 

 

3. 꺼낸 j에 인접항 정점들 중, 아직 방문하지 않은 정점들을 stack에 저장

 

adjacency[0] = {1,2,3}이고 visited[1],visited[2], visited[3]모두 false이므로, stack에 넣어준다.

 

 

 

 

 

4. stack에서 값을 꺼내어 위 2~3번 과정을 반복한다

 

  4.1) stack에서 값 j = 3를  꺼낸 후, 방문처리 

 

4.2) 꺼낸 j = 3에 인접한 정점들 중, 아직 방문하지 않은 정점들을 stack에 저장

adjacency[3] = {0,5}이고 visited[0] = True,visited[5] = False이므로, 5를 stack에 넣어준다.

 

 

 

4.3) stack에서 값 j = 5를  꺼낸 후, 방문처리 

 

 

 

 

4.4) 꺼낸 j = 5에 인접한 정점들 중, 아직 방문하지 않은 정점들을 stack에 저장

adjacency[5] = {2,3,6}이고 visited[3] = True,visited[2] = False ,visited[6] = False이므로, 2와 6을를 stack에 넣어준다.

 

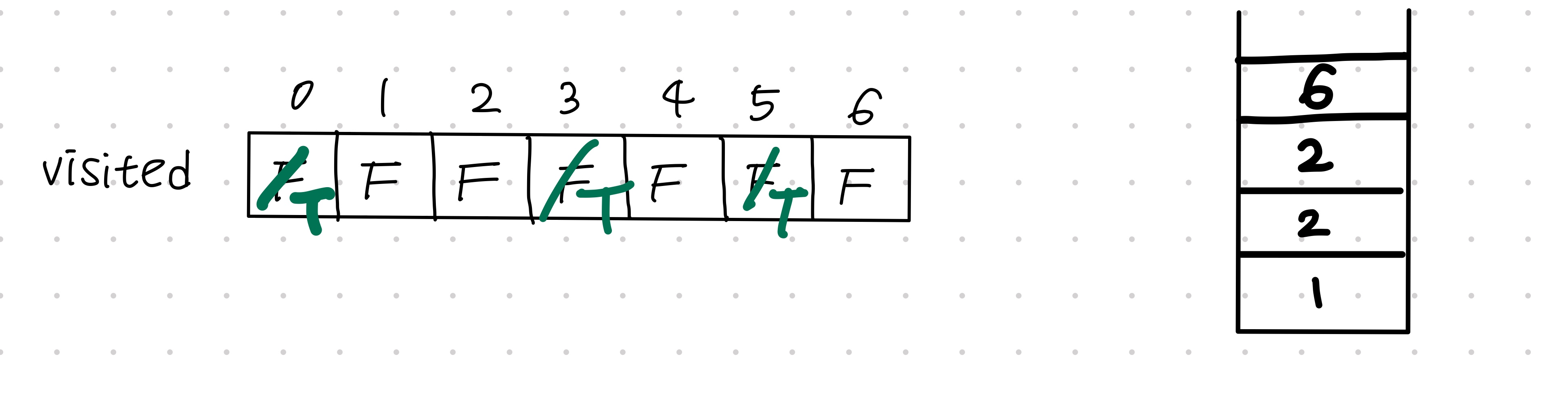
4.5) stack에서 값 j = 6를  꺼낸 후, 방문처리 

 

 

4.6) 꺼낸 j = 6에 인접한 정점들 중, 아직 방문하지 않은 정점들을 stack에 저장

adjacency[6] = {4,5}이고 visited[5] = True,visited[4] = False 이므로, 4를 stack에 넣어준다.

 

4.7) stack에서 값 j = 4를  꺼낸 후, 방문처리 

 

4.8) 꺼낸 j = 4에 인접한 정점들 중, 아직 방문하지 않은 정점들을 stack에 저장

adjacency[4] = {1,2,6}이고 visited[6] = True, visited[1] = False , visited[2] = False 이므로, 1과 2를 stack에 넣어준다.

 

 

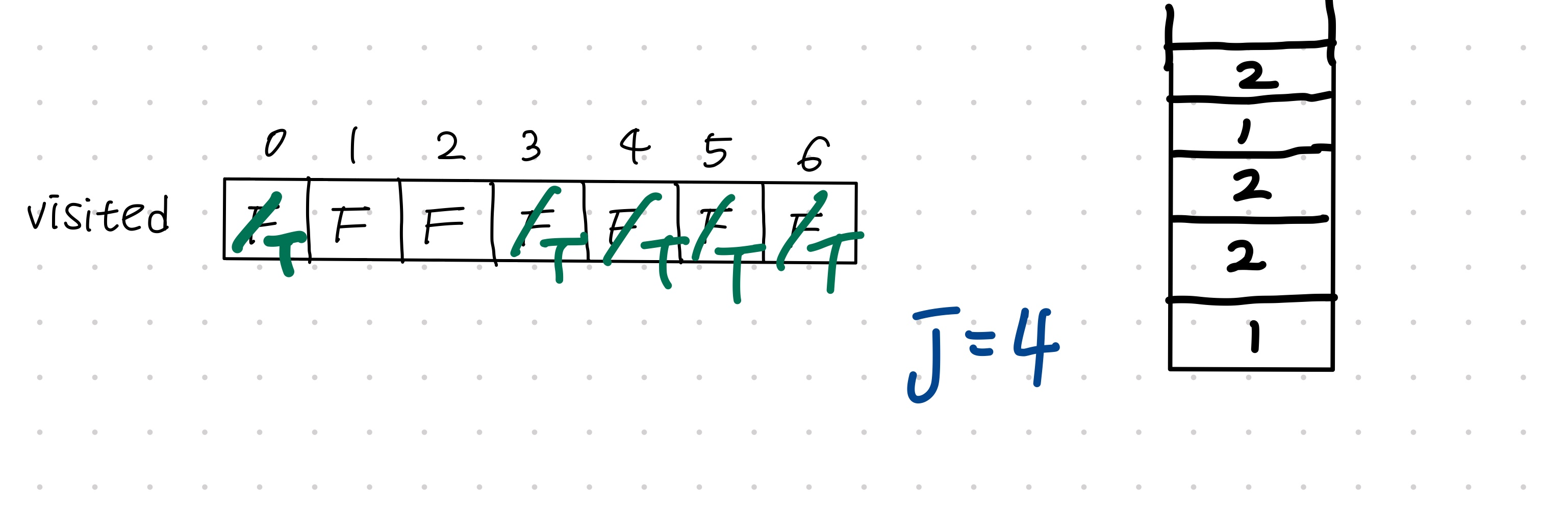
4.9) stack에서 값 j = 2를  꺼낸 후, 방문처리 

 

 

4.10) 꺼낸 j = 2에 인접한 정점들 중, 아직 방문하지 않은 정점들을 stack에 저장

adjacency[2] = {0,1,3}이고 visited[0] = True, visited[1] = False , visited[3] = True 이므로, 1을 stack에 넣어준다.

 

 

4.11) stack에서 값 j = 1를  꺼낸 후, 방문처리 

 

4.12) 꺼낸 j = 1에 인접한 정점들 중, 아직 방문하지 않은 정점들을 stack에 저장

adjacency[1] = {0,4}이고 visited[0] = True, visited[4] = True 이므로, stack에 넣어줄 것이 없다.

 

4.13) stack에서 값 j = 1를  꺼낸 후, 방문처리 -> 이미 방문처리 되어있으므로, skip

 

 

4.14) stack에서 값 j = 2를  꺼낸 후, 방문처리

v

 

 

4.15) 전부 방문 되었으므로, stack이 빌 때까지 계속 pop만 하다가 loop종료

 

 

수도코드

 

코드

C++

#include <iostream>
#include <vector>
#include <stack>
using namespace std;

// DFS 메서드 정의
void dfs(vector<vector<int>>& graph, int start, vector<bool>& visited) {
    stack<int> s;
    s.push(start);
    visited[start] = true;

    while (!s.empty()) {
        int j = s.top();
        s.pop();
        cout << "Visited node: " << j << endl;

        for (int k : graph[j]) {
            if (!visited[k]) {
                s.push(k);
                visited[k] = true;
            }
        }
    }
}

int main() {
    // 그래프 초기화
    vector<vector<int>> graph = {
        {},         // 0번 노드
        {2, 3},     // 1번 노드
        {1, 8},     // 2번 노드
        {1, 4, 5},  // 3번 노드
        {3, 5},     // 4번 노드
        {3, 4},     // 5번 노드
        {7, 8},     // 6번 노드
        {6, 8},     // 7번 노드
        {2, 6, 7}   // 8번 노드
    };

    // 방문 여부를 나타내는 배열 초기화
    int n = graph.size();
    vector<bool> visited(n, false);

    // 시작 정점을 1로 설정
    int start = 1;

    // DFS 실행
    dfs(graph, start, visited);

    return 0;
}

 

Python

◾ 인접 리스트 사용

graph = [
    [],
    [2, 3, 8],
    [1, 7],
    [1, 4, 5],
    [3, 5],
    [3, 4],
    [7],
    [2, 6, 8],
    [1, 7]
]
visited = [0] * 9


def DFS(graph, v, visited):
    visited[v] = 1
    print(v, end = ' ')

    for i in graph[v]:
        if visited[i] == 0:
            DFS(graph, i, visited)


DFS(graph, 1, visited)

 

◾ 인접 행렬 사용

INF = 999999
graph = [
    [INF, INF, INF, INF, INF, INF, INF, INF, INF], # 0
    [INF, INF, 1, 1, INF, INF, INF, INF, 1], # 1
    [INF, 1, INF, INF, INF, INF, INF, 1, INF], # 2
    [INF, 1, INF, INF, 1, 1, INF, INF, INF], # 3
    [INF, INF, INF, 1, INF, 1, INF, INF, INF], # 4
    [INF, INF, INF, 1, 1, INF, INF, INF, INF], # 5
    [INF, INF, INF, INF, INF, INF, INF, 1, INF], # 6
    [INF, INF, 1, INF, INF, INF, 1, INF, 1], # 7
    [INF, 1, INF, INF, INF, INF, INF, 1, INF] # 8
]
visited = [0] * len(graph[0])

def DFS(graph, v, visited):
    visited[v] = 1
    print(v, end=' ')

    for i in range(1, len(graph[0])):
        if visited[i] == 0:
            if graph[v][i] == 1:
                DFS(graph, i, visited)

DFS(graph, 1, visited)