[Dynamic Programming] 조약돌 문제

문제

* 아래 문제의 recursive property를 제시하라.

 

3×N 테이블의 각 칸에 양 또는 음의 정수가 기록되어 있다.

 

조약돌을 놓는 방법 (제약조건)

- 각 열에는 적어도 하나의 조약돌을 놓아야 한다.

- 가로나 세로로 인접한 두 칸에 동시에 조약돌을 놓을 수 없다.

 

목표

돌이 놓인 자리에 있는 수의 합을 최대가 되도록 조약돌 놓기

 

합법적인 예

 

합법적이지 않은 예

 

 

문제풀이 

 다이나믹 프로그래밍

 

- 행렬의 Column 11부터 Column i𝑖 까지의 최적해(=최고점)는
  Column 11부터 Column i−1𝑖−1 까지의 최적해를 포함하는 구조이기 때문이다.

 

 패턴 분석

각각의 Column에 돌을 놓을 수 있는 경우의 수는, 아래와 같이 4가지로 존재한다.

 

 

 

임의의 Pattern에 대해 Compatible한 경우는, 아래와 같다.

 

1. 패턴 1의 이전에 올 수 있는 패턴  => 2가지

 

 

2. 패턴 2의 이전에 올 수 있는 패턴 => 3가지

 

 

3. 패턴 3의 이전에 올 수 있는 패턴 => 2가지

 

 

 

 

4. 패턴 4의 이전에 올 수 있는 패턴 => 1가지

 

 

 

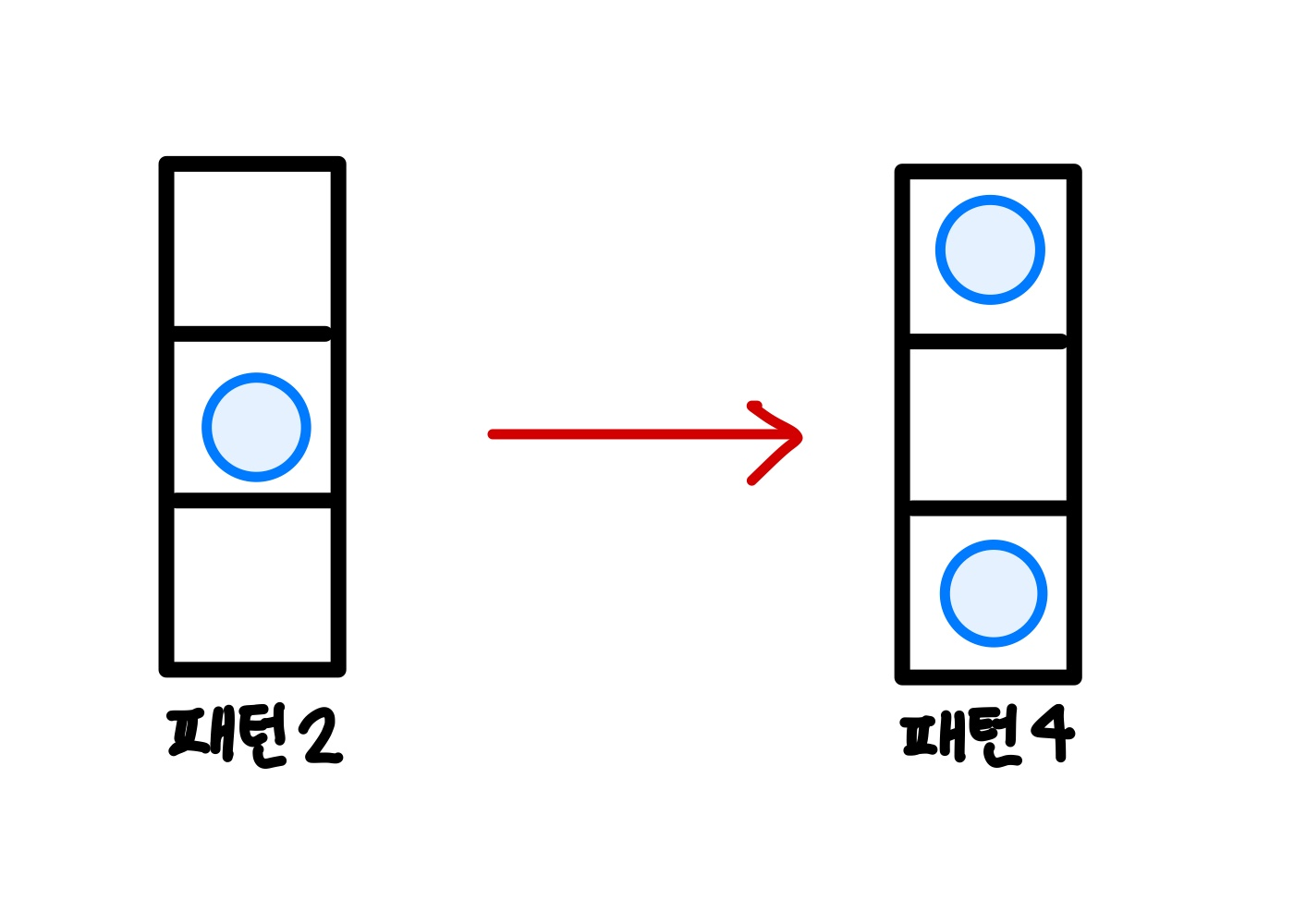
 재귀적 접근

 

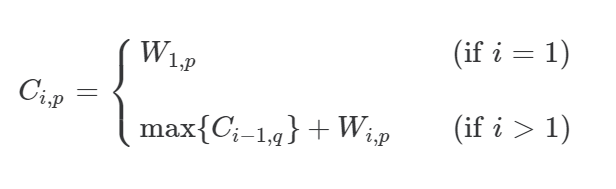
𝐶𝑖,𝑝 : Column  𝑖 에 Pattern 𝑝 로 놓일 경우의 최고 점수

𝑊𝑖,𝑝 : Column 𝑖에 Pattern 𝑝로 놓일 경우, Column 𝑖에 돌이 놓인 곳의 값

 

(이 때, q𝑞는 p𝑝에 Compatible한 Pattern이어야 한다.)

 

최종적으로 3Xn3𝑋𝑛 Matrix에서 Optimal Solution은,
𝐶𝑛,1 ~ 𝐶𝑛,4 중 가장 큰 값이 된다.

 

각 열에 따라 Case에 따른 돌이 놓인 곳의 합을 Value라는 배열에 저장하자.

 

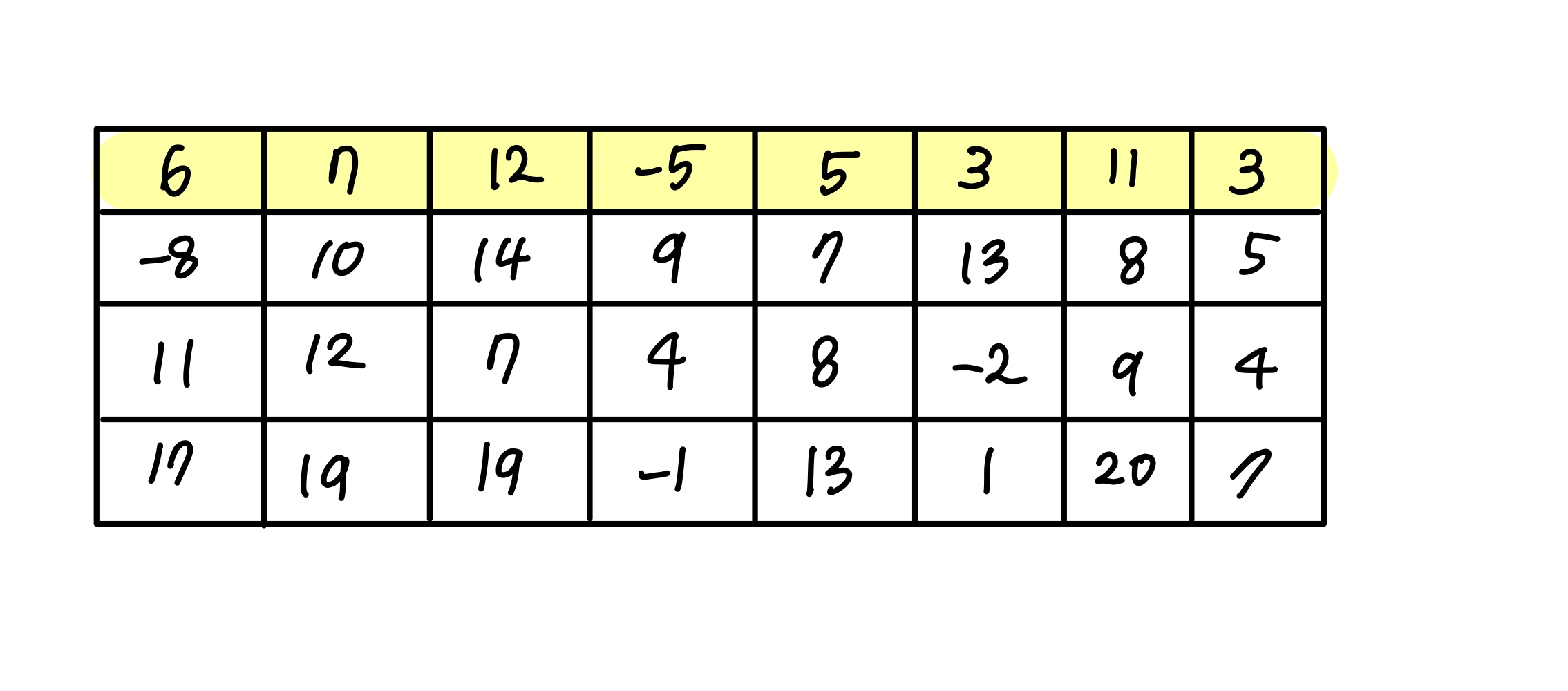
- 주어진 value 배열은 각 열에 특정 Case의 조약돌을 놓았을 때 얻을 수 있는 값을 나타낸다. 목표는 각 열마다 1부터 j까지 조약돌을 놓았을 때 얻을 수 있는 최대값을 구하는 것이다.

 

- 이를 위해서는 각 열 j에서의 경우(Case)에 따라 이전 열 j-1에서 어떤 경우의 조약돌을 놓을 수 있는지를 고려해야 한다.

 

ex) j열에 Case 3의 조약돌을 놓았다면, j-1열에서는 Case 1 혹은 Case 2의 조약돌만 놓을 수 있다. 따라서 이전 열의 가능한 경우 중 최대값을 선택하고, 이 값에 현재 열 j에서의 Case 3의 값을 더하여 최대값을 계산한다.

 

이 과정을 DP(dynamic programming)로 구현하면, dp[j][i]는 j열에 Case i의 조약돌을 놓았을 때 얻을 수 있는 1부터 j까지의 최대값을 나타내게 된다.

 

 

구현 절차를 정리하면 아래와 같다.

1. 초기화: dp[0][i] = 0 (모든 i에 대해)
2. 점화식: dp[j][i] = max(dp[j-1][k] + value[j][i]) (k는 j열에 올 수 있는 모든 경우)
3. 모든 j열과 i에 대해 dp[j][i]를 계산하여 최대값을 구하기

 

코드

C++

#include<iostream>
#include<algorithm>

using namespace std;

int Value[4][100001];
int DP[4][100001];

int main()
{
	int i, j, cnt;

	cin >> cnt;

	// Input
	for (i = 0; i < 3; i++)
	{
		for (j = 0; j < cnt; j++)
		{
			cin >> Value[i][j];
		}
	}

	// 1,3번째 행이 동시에 조약돌이 놓일 때 Value
	for (i = 0; i < cnt; i++)
	{
		Value[3][i] = Value[0][i] + Value[2][i];
	}

	// Case 1. -> Case2,3
	// Case 2. -> Case1,3,4
	// Case 3. -> Case1,2
	// Case 4. -> Case2

	// i번째 열이 Case x일 때, 1~i열 까지의 최대합
	DP[0][0] = Value[0][0];
	DP[1][0] = Value[1][0];
	DP[2][0] = Value[2][0];
	DP[3][0] = Value[3][0];

	for (i = 1; i < cnt; i++)
	{
		DP[0][i] = max(DP[1][i - 1], DP[2][i - 1]) + Value[0][i];
		DP[1][i] = max(max(DP[0][i - 1], DP[2][i - 1]), DP[3][i - 1]) + Value[1][i];
		DP[2][i] = max(DP[0][i - 1], DP[1][i - 1]) + Value[2][i];
		DP[3][i] = DP[1][i - 1] + Value[3][i];
	}

	cout << max(max(max(DP[0][cnt - 1], DP[1][cnt - 1]), DP[2][cnt - 1]), DP[3][cnt - 1]) << endl;

	return 0;
}

 

Python

def max_sum_3n_table(table):
    n = len(table[0])  # 열의 개수 N
    
    # Value 배열 초기화(패턴1,패턴2,패턴3)
    Value = [[0] * n for _ in range(4)] #
    for i in range(3): 
        for j in range(n):
            Value[i][j] = table[i][j]
    
    # 1, 3번째 행이 동시에 조약돌이 놓일 때 Value 계산 (패턴4)
    for j in range(n):
        Value[3][j] = Value[0][j] + Value[2][j]
    
    # DP 배열 초기화
    DP = [[0] * n for _ in range(4)]
    
    # 첫 번째 열 초기화
    DP[0][0] = Value[0][0]
    DP[1][0] = Value[1][0]
    DP[2][0] = Value[2][0]
    DP[3][0] = Value[3][0]
    
    # DP 배열 채우기
    for i in range(1, n):
        DP[0][i] = max(DP[1][i - 1], DP[2][i - 1]) + Value[0][i] #패턴1
        DP[1][i] = max(DP[0][i - 1], DP[2][i - 1], DP[3][i - 1]) + Value[1][i] #패턴 2
        DP[2][i] = max(DP[0][i - 1], DP[1][i - 1]) + Value[2][i] #패턴 3
        DP[3][i] = DP[1][i - 1] + Value[3][i] #패턴 4
    
    # 최대값 반환
    max_sum = max(DP[0][n - 1], DP[1][n - 1], DP[2][n - 1], DP[3][n - 1])
    
    return max_sum

# 예제 사용
table = [
    [6, 7, 12, -5, 5, 3, 11, 3], 
    [-8, 10, 14, 9, 7, 13, 8, 5], 
    [11, 12, 7, 4, 8, -2, 9, 4]
]

print(max_sum_3n_table(table))  # 출력: 최대 합

 

 

• Value 배열:
  • Value 배열은 입력으로 주어진 3xN 크기의 테이블에서 값을 가져와서 계산된 결과를 담는 배열이다.
  • 코드에서는 Value 배열의 크기를 4xN으로 설정하고 있다. 이는 DP 테이블을 채우기 위해 필요한 값들을 저장하는 공간으로 활용된다.
• DP 배열:
  • DP 배열은 Dynamic Programming (DP) 기법을 사용하여 최적해를 저장하는 배열이다.
  • 코드에서는 4xN 크기로 설정되어 있으며, 각 행마다 이전 열까지의 최적해를 저장하고 새로운 열의 최대값을 계산한다.
• table 배열:
  • table 배열은 실제 입력으로 주어지는 3xN 크기의 테이블이다.
  • table[i][j]는 i번째 행, j번째 열의 원소를 의미한다.
  • 초기화 과정에서 Value 배열로 복사되어 각 케이스에 따라 필요한 값들을 계산하거나 사용한다.

 

 

---

Reference

https://dad-rock.tistory.com/623

[Algorithms] Pebble Placement Problem | 돌 놓기 문제

https://jinwoo-jung.com/73

[ DP ] 조약돌 놓기(C++)